CS 6515: Graduate Algorithms

Disclaimer
The views and opinions expressed in this post are solely my own and do not reflect those of Georgia Tech, the OMSCS program, or any affiliated instructors, TAs, or staff.

Instructor: Gerandy Brito
Video Lessons: Eric Vigoda
Head TA: Joves Luo et al
Semester: August 2025
Overall Rating: 👎 Only take if necessary

✅ Pros

• Interesting subject matter
• Studying can be made much more efficient by primarily focusing on homework problems

❌ Cons

• Expectations are not clearly set
• Course communication is overly verbose and difficult to parse
• Grading is nitpicky and overly punitive
• Extremely heavy workload

---

🕒 Time Commitment

15–30 hours per week.

---

📝 Grade Breakdown

Task	Weight	Notes
Quizzes	10%	20 quizzes
Exams	90%	3 hours long

📚 Course Content

📘 Primary Textbook: Algorithms by Dasgupta, Papadimitriou, Vazirani (DPV)

✍️ Homeworks

There are two types of homework assignments:

1. Written homework with one graded problem, a written submission, and additional practice problems from DPV
2. Programming assignments

The first type is essential for success in the class. While homework is technically ungraded, it is critical to submit in order to understand the grading rubric. Every graded-style problem should be thoroughly memorized.

Get your hands on a student’s perfect submission, people typically post these on Ed. These are often the only solutions that align with how exam problems are graded, and these problem types will show up on the exams.

📄 Exam 1: Dynamic Programming + Divide and Conquer

Dynamic Programming (DP)

See a visualization of DP programs running step-by-step here

Solution Structure

1. Subproblem Definition
   Build on a subset of the input (e.g., A[1..i]). Subproblems are described in words:
   “T(i, j) is the …”

2. Recurrence Definition
   Provide a mathematical definition of the table entries. The subproblem definition explains the meaning in English; the recurrence defines it formally.

3. Implementation Analysis: Is an assessment of building and using this table defined in the “recurrence relation” to solve the original problem.
   • State the number of subproblems in big-O notation
   • State the runtime to fill this table
   • State how/where the final return is extracted from that table
   • State the runtime to extract the final return in big-O notation

Must Know

• Longest Common Subsequence
• Longest Common Substring
• Knapsack (Without Repetition)
• Knapsack (With Repetition)
• Edit Distance
• Longest Increasing Subsequence (LIS)
• Longest Increasing Substring
• Chain Matrix Multiply
• Shortest Paths

Example Problems

• DPV 6.1 Max sum contiguous subsequence (substring)
• DPV 6.2 Hotel stops
• DPV 6.3 Yuckdonald’s
• DPV 6.4 Corrupted Text Document
• DPV 6.5 Pebbling a checkerboard
• DPV 6.6 *Multiplication operation on three symbols a, b, c
• DPV 6.7 Longest palindromic subsequence
• DPV 6.8 Longest common substring
• DPV 6.9 String-processing language
• DPV 6.11 Longest common subsequence
• DPV 6.17 Making Change A
• DPV 6.18 Making Change B
• DPV 6.19 Making Change C
• DPV 6.20 Optimal BST
• DPV 6.22 Does some subset of the ai’s add up to t?
• DPV 6.26 Alignment

• Checkerboard
  You are given a checkerboard with n rows and n columns. This is just an n x n table V. The (i, j) entry of V has value v(i, j) (Can be positive or negative). We want to move a checker from the top-left corner (i.e., position (1, 1)) to the bottom-right (i.e., position (n, n)). The only legal moves are to move a checker down by one square (i, j) -> (i + 1, j), right by one square (i, j) -> (i, j + 1), or diagonally down-right by one square (i, j) -> (i + 1, j + 1). The value of a sequence of moves is the sum of the values of the entries in the sequence. We want the maximum value of any legal sequence of moves. Here is an example of a 3 x 3 checkerboard:

                1    2    3
      
        1   [   3,  30,  12 ]
        2   [ -12,   7,  -9 ]
        3   [  39,  -2,  15 ]
  

  The sequence of moves (1, 1) -> (1, 2) -> (2, 2) -> (3, 3) is legal and has total value 3 + 30 + 7 + 15 = 55.

  Give a dynamic programming algorithm that given the values V determines the maximum value of any legal sequence of moves from (1, 1) to (n, n). You just need to output the total value from the optimal solution.

• Longest Common Sub!?
  Given two strings X = x_1, x_2,…,x_n and Y = y_1, y_2,…,y_m we want to find the length of the longest string Z = z_1,…,z_k where Z appears as a substring of X and as a subsequence of Y. Recall, a substring is consecutive elements.

  For example, for the following input:

        X = a, b, d, b, a, b, f, g, d
        Y = b, e, t, f, d, b, f, a, f, r
  

  The answer is 4 (since b, d, b, a is a substring of X and it is also a subsequence of Y).

• Max-Sum Common Substring
  Given two sequences of n numbers: X = x_1, x_2,…,x_n and Y = y_1, y_2,…,y_n. We want to find the sequence Z = z_1,…,z_k which appears as a substring of X and Y, and which has maximum sum. Design a dynamic programming algorithm for this problem. You only need to output the maximum sum, you don’t need to output the substring.

  For example, for the following input:

        X = 5, 2, 7, -1, 6, -4, 9, 2, -3, 1
        Y = 7, -1, 6, -4, 5, 5, 1, -1, 9, 2
  

  then the answer is 12 (using substring 7, -1, 6)

• Subset Sum
  Given a list a_1, a_2,…,a_n of positive integers, and a positive integer k, give a dynamic programming algorithm that determines if there exists a subset S of indices {1, 2,…,n} such that

    ∑ a_i = k
    i∈S
  

  Note each index can be used at most once. Your algorithm just needs to output YES or NO Example: A = [2, 5, 7, 1, 12] for k = 21, the answer is YES (using S = {1, 3, 5}); for k = 16, the answer is NO

• Knapsack by value
  There are n items with integer weights w_1,…,w_n and integer values v_1,…,v_n, and total capacity B. Find the maximum value from a subset of objects that fits in the backpack. (One copy of each object)

  Let V = ∑_i v_i = total value of all objects

• Electoral College
  There are n states labelled 1, 2,…,n. Each state has an integer population p_i > 0 and an integer number of votes v_i > 0 allocated to that state (the votes are not necessarily proportional to the population). The problem is to determine the set of states with the smallest total populations that can provide the votes to exceed a given threshold. Formally, the problem is the following:

  Let p_i be the population of state i, and v_i the number of votes for state i. All votes of a state go to a single candidate, and the winning candidate is the one who receives at least Z electoral votes. You are given as input: n, Z, p_1,…,p_n; and v_1,…v_n. Your goal is to find a set of states S with the smallest total population that has at least Z electoral votes in total. You only have to output the total population of the set S, you do not need to output the set S itself.

  For example, if n = 5, population P = [200, 100, 30, 700, 250], votes V = [5, 1, 2, 7, 6] and Z = 12 then the solution is 480 since 480 = 200 + 30 + 250 and states 1, 3, 5 have 5 + 2 + 6 = 13 electoral votes.

  Note in this example: p_2 > p_3 but v_2 < v_3, this might occur, but shouldn’t affect your algorithm. Design a dynamic programming algorithm for this problem.

• Palindrome partitions
  Any string can be broken into a sequence of palindromes. For example, the string “BUBBASEESABANANA” can be broken up in several ways:

    BUB * BASEESAB * ANANA
    B * U * BB * ASEESA * B * ANANA
    BUB * B * A * SEES * ABA * N * ANA
    B * U * B * B * A * S * E * E * S * A * B * A * N * A * N * A
  

  Given a string X = x_1,…,x_n find the minimum number of palindromes that X can be partitioned into.

• Forward-Backward String
  Describe and analyze and efficient algorithm to find the length of the longest contiguous substring that appears both forward and backward in an input string T[1,…,n]. The forward and backward substrings must not overlap.

  Here are several examples:

  • Given the input string ALGORITHM, your algorithm should return 0
  • Given the input string RECURSION, your algorithm should return 1, for the substring R
  • Given the input string REDIVIDEm your algorithm should return 3, for the substring EDI (Forward and backward strings should not overlap!)
  • Given the input string DYNAMICPROGRAMMINGMANYTIMES, your algorithm should return 4, for the substring YNAM. (In particular it should not return the substring 6, for the sequence YNAMIR).

• Adding Parenthesis
  Suppose you are given a sequence of integers separated by + and x signs;

  For example, 1 + 3 x 2 x 0 + 1 x 6 + 7

  You can change the value of this expression by adding parenthesis in different places. For example:

    (1 + (3 x 2)) x 0 + (1 x 6) + 7 = 13
    ((1 + (3 x 2 x 0) + 1) x 6) + 7 = 19
    (1 + 3) x 2 x (0 + 1) x (6 + 7) = 104
  

  (a) Describe and analyze an algorithm to compute the maximum possible value the given expressions can take by adding parenthesis, assuming all integers in the input are positive. [Hint: This is easy]
  (b) Describe and analyze an algorithm to compute the maximum possible value the given expressions can take by adding parenthesis, assuming all integers in the input are non-negative.
  (c) Describe and analyze an algorithm to compute the maximum possible value the given expressions can take by adding parenthesis, with no restrictions on the input numbers. Assume any arithmetic operation take O(1) time. —

Divide and Conquer (D&C)

Solution Structure

1. Algorithm: Describe how the algorithm works in words
2. Correctness: Explain why it works
3. Runtime Analysis: Worst-case Big-O analysis

Must Know

• Binary Search
• Merge Sort
• Median of Medians (FastSelect)
• FastMultiply

Example Problems (DPV)

• 2.1 (Practice fast multiplication)
• 2.5 (Solving recurrence)
• 2.16 (infinite array)
• 2.23 (majority element)
• 2.4
• 2.12
• 2.15
• 2.17-2.20
• 2.22 (you should devise two solutions: a straightforward Median of medians application and a “merging” approach.)
• 2.27-2.28 (if you are curious about further extensions of the Fast Multiplication Algorithm)
• 2.32 (a very nice application of D&C in a geometric setting, this problem is harder and its runtime analysis is above what we have covered in class so far)
• Binary search modified
  Design an O(log(n)) algorithm to find the smallest missing natural number in a given sorted array of length n. The given array only has distinct natural numbers. For example, the smallest missing natural number from A = [3, 4, 5] is 1, and from A = [1, 3, 4, 6] is 2.

---

📄 Exam 2: Graph Theory

Solution Structure

1. Algorithm: Describe “how” to solve the problem in words (narrative/paragraph form)
2. Justification of Correctness: Describe “why” your algorithm solves the problem
3. Runtime Analysis: Analyze all steps of the algorithm in worst case Big-O notation

Must Know

• Strongly connected components (SCCs)
• Minimum Spanning Trees (MSTs)
• Depth-First Search (DFS)
• Breadth-First Search (BFS)
• Topological Sort
• Dijkstra’s
• Bellman-Ford (BF)
• Floyd-Warshall
• Kruskal’s
• Prim’s
• Ford-Fulkerson
• Edmonds–Karp
• 2-SAT
• Max-flow min-cut theorem

Example Problems

• DPV 3.1: “Perform a depth-first search on the following graph…”
• DPV 3.2: “Perform depth-first search on each of the following graphs…”
• DPV 3.7(a-c): “A bipartite graph is a graph…”
• DPV 3.8: “Pouring Water”
• DPV 3.11: “Design a linear-time algorithm…”
• DPV 3.16: “Suppose a CS curriculum…”
• DPV 3.22: “Give an efficient algorithm which takes as input a directed graph G=(V,E)…”
• DPV 3.24: “Give a linear-time algorithm for the following task.”
• DPV 4.1: “Suppose Dijkstra’s algorithm is run…”
• DPV 4.2: “Just like the previous problem, but this time with the Bellman-Ford algorithm.”
• DPV 4.3: “Squares.”
• DPV 4.8: “Professor F. Lake suggests…”
• DPV 4.11: “Give an algorithm that takes as input a directed graph with positive edge lengths…”
• DPV 4.12: “Give an O(∣V∣^2) algorithm…”
• DPV 4.13: “You are given a set of cities…”
• DPV 4.20: “There is a network of roads G=(V,E)…”
• DPV 4.21: “Shortest path algorithms can be applied in currency trading.”

---

📄 Exam 3: NP Theory + Linear Programming

NP Proofs

Solution Structure

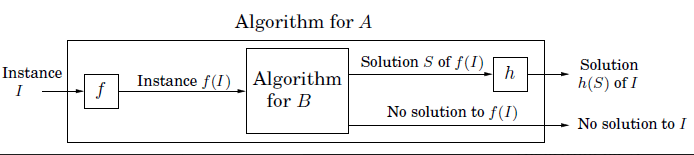
1. First we show that problem B is in the class NP by demonstrating we can verify the candidate solution to B in polynomial time. Check properties of the candidate solution All checks on the candidate solution are polynomial in the input size so problem B is in the class NP.

2. Reduction Next we show that problem B is in the class NP-complete by reducing problem A → B.

   • Input Transformation: Given an instance of problem A (in_1,…in_n) we transform the input to problem A to an input to problem B. Describe input transformation and runtimes. All input transformations are polynomial in the input size.

   • Output transformation: If B has NO solution then A has NO so we return NO for A. If B has a solution we transform the output of B as follows… Next, describe the output transformation and runtimes

3. Correctness Justification: Argue both directions (or their logical equivalents)

   • If there is a solution to B there is a solution to A
   • If there is NO solution to B there is NO solution to A

Must Know

• SAT
• 3-SAT
• Clique
• Independent Set (IS)
• Vertex Cover (VC)
• Subset Sum (SSS)
• Rudrata Path (Hamiltonian Path)
• Rudrata (s, t)-Path
• Rudrata Cycle
• Traveling Salesman Problem (TSP)
• Integer Linear Programming (ILP)
• Zero-One Equations (ZOE)
• 3D Matching

Example Problems

• DPV 8.6: “On page 251 we saw that 3SAT 3SAT remains NP-Complete…”
• DPV 8.10(b-f): “Proving NP-Completeness by generalization.”
• DPV 8.13(a-d, f): “Determine which of the following problems are NP-Complete…”
• DPV 8.14: Clique & Independent Set
• DPV 8.15: Maximum Common Subgraph
• DPV 8.17: problem Π
• DPV 8.20: Dominating Set
• DPV 8.22: Feedback Arc Set

---

Linear Programming

This is very straightforward content compared to the rest of the class content and was not weighted heavily toward the final grade.

A complete linear program has three components:

• An objective function which maximizes or minimizes a linear equation
• A set of constraints which must be met to satisfy the linear program
• A set of non-negativity constraints, one for each variable of the equation

💬 Class Participation & Interaction

Ed is not optional. Key clarifications and grading expectations are communicated there, and closely following Ed threads is required to do well. Many important details are only revealed through these discussions, and students who do not monitor them closely are at a huge disadvantage.

💭 Final Thoughts

I’m conflicted about this course. The material itself is among the most intellectually stimulating in the program. It develops strong algorithmic intuition and forces a level of rigor that is genuinely valuable for long-term growth.

That said, the grading is overly pedantic and exacting in ways that can feel detrimental to the learning objectives. Small deviations in structure or wording, rather than conceptual misunderstanding, can meaningfully impact scores, which is particularly frustrating in a course where exam performance largely determines whether a student passes or fails. This dynamic adds a level of stress that frequently detracts from the learning objectives.

Joves stood out as an exceptional TA. His clarity, and willingness to hold extensive office hours (often exceeding four hours at a time) materially improve the course experience. He consistently bridges the gap between theoretical expectations and practical exam execution. Without his support, the course would be substantially worse.

Ultimately, this is a course I would only recommend to students who need this to complete the program. For those who can adapt to the disorderly and unclear demands, CS 6515 can be tolerable, but it requires patience, precision, and a high tolerance for frustration.